Training LLaMA 3 on TPUs
Part 6 of How To Scale Your Model (Part 5: Training | Part 7: Inference)
Let's take a close look at how we'd train LLaMA 3 models on TPU v5p using what we've learned in the previous section. How big are they? How expensive is training in different configurations? How are they sharded? Let's work through some back-of-the-envelope estimates for how the previous sections map onto real models.
What Does LLaMA 3 Look Like?
The LLaMA-3 model family
| hyperparam | value |
|---|---|
| \(n_\text{layers}\) (L) | 80 |
| \(d_\text{model}\) (D) | 8,192 |
| \(\text{ffw}_\text{multiplier}\) (F // D) | 3.5 |
| \(n_\text{heads}\) (N) | 64 |
| \(n_\text{kv_heads}\) (K) | 8 |
| \(d_\text{qkv}\) (H) | 128 |
| \(n_\text{embeddings}\) (V) | 128,256 |
To highlight how easy this is to find, here’s the config itself, along with a mapping:
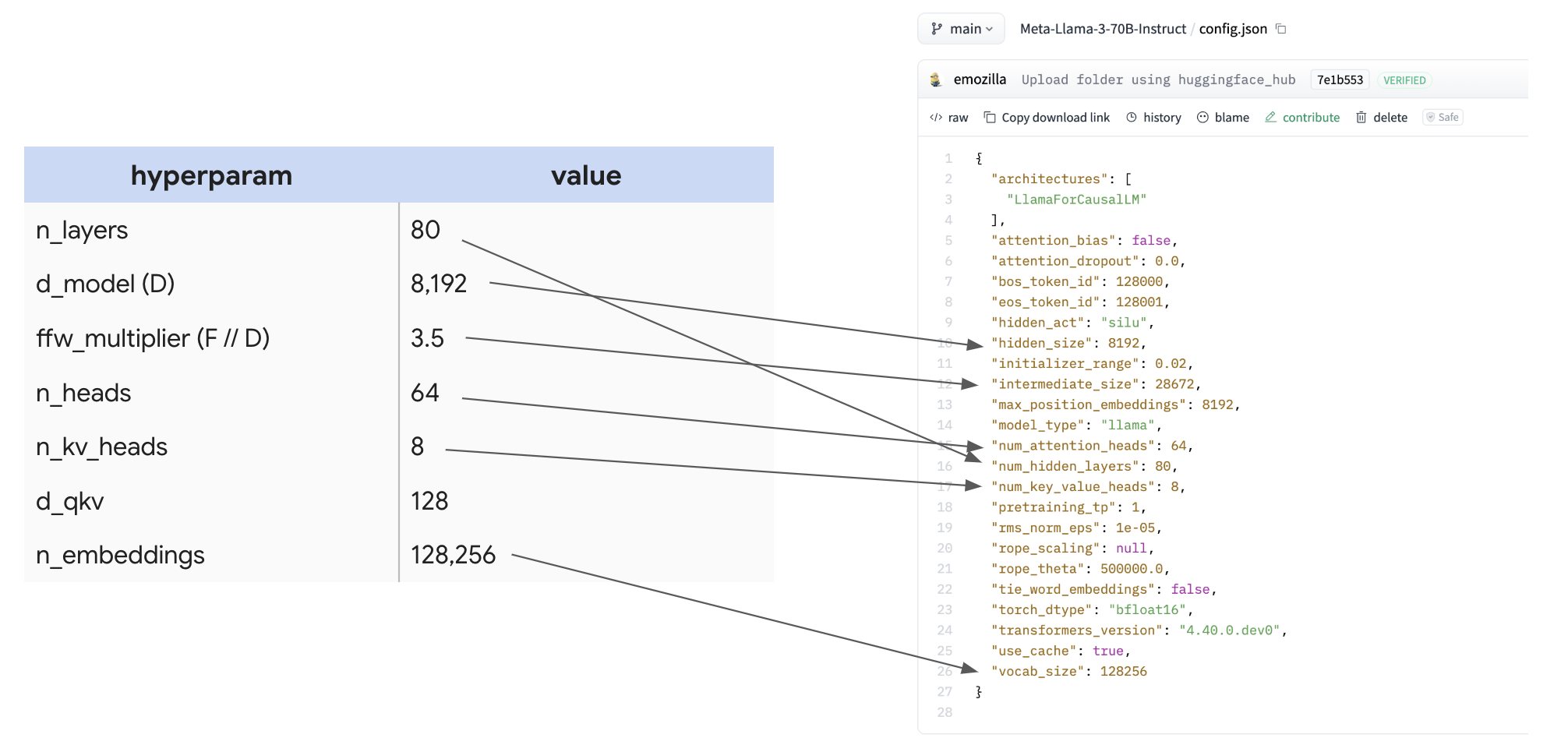
It’s useful to make a big table with these numbers for many different open-source LLMs, so you can quickly compare the design decisions they’ve made.
Counting Parameters and FLOPs
Question: From this table, can we calculate the LLaMA 3-70B parameter count? 🤫 Let’s apply the content of Section 4 and see if we can get 70B!
| param | formula | count |
|---|---|---|
| FFW params | d_model * d_model * ffw_multiplier * 3 (for gelu + out-projection) * n_layers | 8,192 * 8,192 * 3.5 * 3 * 80 = 56.3e9 |
| Vocab params | 2 (input and output embeddings) * n_embeddings * d_model | 2 * 128,256 * 8,192 = 2.1e9 |
| Attention params | n_layers * [ 2 (for q embedding and concatenated output projection) * d_model * n_heads * d_qkv + 2 (for k and v) * d_model * n_kv_heads * d_qkv] | 80 * (2 * 8,192 * 64 * 128 + 2 * 8,192 * 8 * 128) = 12e9 |
| 56.3e9 + 2.1e9 + 12e9 = 70.4e9 |
That’s great! We get the number we expect. You’ll notice as expected that the FFW parameters totally dominate the overall parameter count, although attention is non-trivial.
Takeaway: The 3 big weight matrices in the MLP block are so much larger than all the other arrays in the Transformer that we can typically almost ignore all other parameters when reasoning about model memory or FLOPs. For LLaMA 3-70B, they represent 56B of 70B parameters.
Question: What about FLOPs? How many FLOPs do we perform per token per training step? This helps us determine how expensive the whole training process will be.
Click here for the answer, once you’ve thought about it!
Answer: As shown in Section 4, we do roughly \(6 \cdot \text{param count}\) FLOPs per token, so here that’s roughly 6 * 70e9 = 4.2e11 FLOPs / token. That’s about half a TFLOP per token per step. Assuming we’re compute-bound, this should take roughly 4.2e11 / 4.59E+14 = 1ms on a single TPU v5p chip, assuming perfect FLOPs utilization.
Question: LLaMA 3 was trained for about 15 trillion tokens. How many FLOPs is that total?
Click here for the answer, once you’ve thought about it!
Answer: That’s easy, it’s just 4.2e11 * 15e12 = 6.3e24 FLOPs total. 6.3 yottaFLOPs. That’s a lot! On a single TPU this would take 6.3e24 / 4.59E+14 = 435 years. That’s also a lot!
Question: Let’s say we wanted to train on a full TPU v5p pod with 16x20x28 = 8960 chips. How long would this take to train at 40% MFU in bfloat16, assuming we are compute-bound?
Click here for the answer, once you’ve thought about it!
Answer: We know that each TPU v5p can perform 4.59e14 FLOPs / second. At 40% MFU, this will take about T = 6.3e24 / (8960 * 4.59e14 * 0.4) = 3.8e6 seconds. This is about 44 days! That’s fairly reasonable, assuming we can actually achieve 40% MFU.
Question: LLaMA 3-70B was pretrained with a batch size of about 4M tokens. How many TPUs do we need at minimum to train with this batch size? While this isn’t that relevant of a question, it gives us a ballpark for the minimum compute resources to train a model like this yourself.
Click here for the answer, once you’ve thought about it!
Answer: This question is primarily asking about memory usage, since that’s the only strict constraint on available compute. During training, we have three primary uses of HBM: model parameters, optimizer state, and gradient checkpoints. If we assume bfloat16 weights, float32 optimizer state, and a very conservative gradient checkpointing scheme (3 times per layer), we have:
| Params | 2 * 70GB | ~140GB |
|---|---|---|
| Optimizer State | 8 * 70GB | ~560GB |
| Gradient Checkpoints | 2 * 8192 * 4e6 * 3 * 80 | ~15.8TB |
| Total | ~16.5TB |
You notice that gradient checkpointing strongly dominates the memory picture, even with a very conservative checkpointing scheme. We could technically go to 1 checkpoint per layer, or do microbatching, but this is a reasonable picture. With these assumptions, since each TPU v5p has 96GB of HBM, we need 16.5e12 / 96e9 = 171 TPUs. That’s not very much actually!
Why wouldn’t we do this? Well, because it would take us 44 days * 8960 / 171 = 2305 days to train. That’s 6 years. That’s a lot. Still, this makes it clear that we’re using these large clusters not because we’re bound by memory but rather because we need the extra FLOPs.
Question: If we do use 8960 TPU v5p chips, how much memory will we use per-chip?
Click here for the answer, once you’ve thought about it!
Answer: Our total memory is still about 16.5TB, so per-chip we’ll be using about 1.8GB per chip, which is bascially nothing. If we did much more aggressive checkpointing, e.g. 12 checkpoints per layer, we’d still only be at 8GB per chip. We’re nowhere near being memory bound during training at these scales.
Takeaways: It is technically possible to train even very large models on very small topologies, with the caveat that they will likely take a long time. Being able to calculate the total FLOPs of a training run allows us to ballpark its training time by assuming a modest MFU and a known topology.
How to Shard LLaMA 3-70B for Training
Let’s stick to our setting from above and say we want to train LLaMA 3-70B with 4M token batch size (1024 sequences of length 8192 per batch) on a TPU v5p pod of 8960 chips. Let’s discuss what the best sharding strategy is for this model.
Question: Can we just do pure FSDP? This should be the first idea you have, since it’s simple and will introduce no extra communication if it works.
Click here for the answer, once you’ve thought about it!
Answer: This depends a bit on our sequence length and what we mean by FSDP. LLaMA 3-70B is initially trained with sequences of length 4K, so at this sequence length a batch size of 4M tokens gives us a sequence batch size of 1024. That means we can only really do pure data parallelism/FSDP up to 1024 chips. So the answer in the simple sense of “pure data parallelism with no extra communication” is no. The next question will answer a slightly less pedantic version of this.
Question: If we allow ourselves to do some sequence sharding, can we do only FSDP? By sequence sharding, we mean splitting our batches along the sequence dimension as well as the batch dimension. This can be seen as almost equivalent to FSDP except for some additional communication complexity during attention when we’ll need to gather the queries or keys. Let’s ignore that here and just think of it as a “token-level” data parallelism strategy.
Click here for the answer, once you’ve thought about it!
Answer: Sequence sharding lets us do more data parallelism by sharding the batch along the sequence dimension as well. This adds some non-trivial communication overhead to attention, but is otherwise equivalent to FSDP. If we did this, we would end up with a per-TPU batch size of 4 * 1024 * 1024 / 8960 = 468 tokens. We said in the previous section that we become ICI-bound by FSDP when \(\text{per device batch size} < 2550 / n_\text{axes}\). Since we could dedicate 3 axes here with a full 3D pod, this would give us a lower bound of 850, which we’re well below. So the answer is no, even with 3 axes.
Question: Let’s give up on pure FSDP and explore mixed tensor parallelism and FSDP. Does this let us remain compute-bound? What amount of FSDP and tensor parallelism should we do?
Click here for the answer, once you’ve thought about it!
Answer: First let’s check to see if this will even fit. We know that we’ll be comms-bound if our per-chip batch size is less than \(2 \cdot 2550^2 / F = 453\). As we saw above, we’re slightly above this. So that’s great! Now to pick the optimal amount of FSDP, we can use the formula
\[X_{opt} = \sqrt{\frac{2BN}{F}} = \sqrt{\frac{2 \cdot 4.19e6 \cdot 8960}{28672}} = 1618\]Rounding to a reasonable multiple of 2, that gives us roughly 2048-way FSDP and 4-way model parallelism. That should work well!
Question: Are we going to be ICI bound with this amount of tensor parallelism? Go through the work of checking how much tensor parallelism we can get away with for LLaMA 3.
Click here for the answer, once you’ve thought about it!
Answer: We basically know the answer is no because the discriminant above was non-negative, but we would become ICI bound for FSDP + tensor parallelism when \(\text{BS per device} < 2 \cdot 2550^2 / F = 453\), so we expect not. We would be ICI bound with pure model parallelism when \(Y > F / 2550 = 11\), which we are well below. So we are not ICI bound here.
Takeaways: We can train LLaMA-3 with a 4M token batch size on a full TPU v5p pod with a mixture of data parallelism (1024-way), sequence parallelism (2-way), and tensor parallelism (4-way) without being communication-bound. We will be comms-bound if we try to do pure FSDP or FSDP + sequence parallelism. The equations we’ve cooked up in the previous section are very practical.
Worked Problems
Question 1 [Scaling LLaMA 70B to more chips]: say we want to train LLaMA 3-70B on 4 pods with the same batch size. What parallelism scheme would we use? Would we be compute or communication bound? Roughly how long would it take to train? Make sure to use the correct roofline bound.
Question 2 [LLaMA 405B]:
(a) Using the LLaMA 3-405B config, write a table with all the key hyperparameters as above. How many total parameters does this model have? How many FLOPs per training step? How many FLOPs do we perform if we train for 15T tokens?
(b) Assume we want to train on 8 TPU v5p pods. What parallelism scheme would we use? How long would training take? Would be compute or comms bound?